Pengertian, Teori, Konsep, Tujuan Jenis dan Hukum Materi Himpunan

Penjelasan Dasar

Dalam kehidupan nyata, banyak sekali masalah yang terkait dengan data (objek) yang dikumpulkan berdasarkan kriteria tertentu. Kumpulan data ini merupakan representasi dari suatu kondisi, baik secara statistika maupun secara ekonomi. Kumpulan data inilah yang selanjutnya didefinisikan sebagai himpunan. Pada bab awal ini akan dibahas tentang definisi dan keanggotaan suatu himpunan, operasi himpunan dari beberapa jenis himpunan.

Tujuan

1. Mahasiswa memahami konsep dasar tentang himpunan.
2. Mahasiswa memahami berbagai macam operasi dan sifat himpunan.
3. Mahasiswa dapat meyelesaikan berbagai persoalan dan fenomena yang terkait dengan teori himpunan.

Definisi dan Keanggotaan Suatu Himpunan

Himpunan (set) merupakan sekumpulan objek-objek yang berbeda yang dapat didefinisikan dengan jelas. Objek di dalam himpunan dinamakan unsur atau anggota himpunan. Keanggotaan suatu himpunan dinyatakan oleh notasi ’∈’.

Contoh 1 :

A = {x, y, z}
x ∈ A : x merupakan anggota himpunan A.
w ∉ A : w bukan merupakan anggota himpunan A.
Ada beberapa cara dalam menyatakan himpunan, yaitu :

a. Mencacahkan anggotanya (enumerasi)

Dengan cara ini, himpunan tersebut dinyatakan dengan menyebutkan semua

anggota himpunannya di dalam suatu kurung kurawal.

Contoh 2 :

• Himpunan empat bilangan ganjil pertama: A = {1, 3, 5, 7}.
• Himpunan lima bilangan prima pertama: B = {2, 3, 5, 7, 11}. 
• Himpunan bilangan asli yang kurang dari 50 : C = {1, 2, ..., 50}
• Himpunan bilangan bulat ditulis sebagai {…, -2, -1, 0, 1, 2, …}.

b. Menggunakan simbol standar (baku)

Suatu himpunan dapat dinyatakan dalam suatu simbol standar (baku) yang telah diketahui secara umum oleh masyarakat (ilmiah).

Contoh 3 :

N = himpunan bilangan alami (natural) = { 1, 2, ... }

Z = himpunan bilangan bulat = { ..., -2, -1, 0, 1, 2, ... }

Q = himpunan bilangan rasional

R = himpunan bilangan riil

C = himpunan bilangan kompleks

Himpunan yang universal (semesta pembicaraan) dinotasikan dengan U.

Contoh 4 :

Misalkan U = {1, 2, 3, 4, 5} dan A = {1, 3, 5} merupakan himpunan bagian dari U.

c. Menuliskan kriteria (syarat) keanggotaan himpunan

Suatu himpunan dapat dinyatakan dengan cara menuliskan kriteria (syarat)
keanggotaan himpunan tersebut. Himpunan ini dinotasinya sebagai berikut :
{ x ⎥ syarat yang harus dipenuhi oleh x }
Contoh 5 :
(i) A adalah himpunan bilangan asli yang kecil dari 10
A = { x | x ≤ 10 dan x ∈ N } atau A = { x ∈ N | x ≤ 10 }
yang ekivalen dengan A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(ii) M = { x | x adalah mahasiswa yang mengambil kuliah matematika diskrit}
Atau
M = { x adalah mahasiswa | ia mengambil kuliah matematika diskrit}}

d. Menggunakan Diagram Venn

Suatu himpunan dapat dinyatakan dengan cara menuliskan anggotanya

dalam suatu gambar (diagram) yang dinamakan diagram venn.

Contoh 6 :

Misalkan U = {1, 2, …, 7, 8}, A = {1, 2, 3, 5} dan B = {2, 5, 6, 8}.

Diagram Venn:

Terkait dengan masalah keanggotaan, suatu himpunan dapat dinyatakan sebagai anggota himpunan lain.

Contoh 7 :
a. Misalkan, M = { mahasiswa STT Telkom }
M1 = { mahasiswa anggota himatel}
M2 = { mahasiswa anggota HMTI}
M3 = { mahasiswa anggota HMIF}
Dengan demikian, M = { M1, M2, M3 }
b. Bila P1 = {x, y}, P2 = { {x, y} } atau P2={P1},
Sementara itu, P3 = {{{x, y}}}, maka x ∈ P1 dan y ∉ P2,
sehingga P1 ∈ P2 , sedangkan P1 ∉ P3, tetapi P2 ∈ P3
Jumlah unsur dalam suatu himpunan dinamakan kardinalitas dari himpunan tersebut. Misalkan, untuk menyatakan kardinalitas himpunan A ditulis dengan notasi:
n(A) atau ⎢A ⎢

Contoh 8 :
(i) B = { x | x merupakan bilangan prima yang lebih kecil dari 10 },
atau B = {2, 3, 5, 7 } maka ⏐B⏐ = 4
(ii) A = {a, {a}, {{a}} }, maka ⏐A⏐ = 3

Jika suatu himpunan tidak mempunyai anggota, dengan kata lain dengan kardinalitas himpunan tersebut sama dengan nol maka himpunan tersebut dinamakan himpunan kosong (null set). Notasi dari suatu himpunan kosong adalah : ∅ atau {}

Contoh 9 :
(i) P = {Mahasiswa Teknik Industri STT Telkom yang pernah ke Mars},
maka n(P) = 0
Jadi P = ∅
(ii) A = {x | akar persamaan kuadrat x2 + 1 = 0 dan x ∈ R}, maka n(A) = 0
Jadi A = {}
(iii) B = {{ }} dapat juga ditulis sebagai B = {∅}.
Jadi B bukan himpunan kosong karena ia memuat satu unsur yaitu himpunan
kosong.
Himpunan A dikatakan himpunan bagian (subset) dari himpunan B jika dan hanya jika setiap unsur A merupakan unsur dari B. Dalam hal ini, B dikatakan superset dari A.
Notasi himpunan bagian : A ⊆ B atau A ⊂ B
Jika digambarkan dalam bentuk diagram Venn himpunan bagian tersebut menjadi :









Contoh 10 :
(i) N ⊆ Z ⊆ R ⊆ C
(ii) {2, 3, 5} ⊆ {2, 3, 5}
Untuk setiap himpunan A berlaku hal-hal sebagai berikut:
(a) A adalah himpunan bagian dari A itu sendiri (yaitu, A ⊆ A).
(b) Himpunan kosong merupakan himpunan bagian dari A ( ∅ ⊆ A).
(c) Jika A ⊆ B dan B ⊆ C, maka A ⊆ C
∅ ⊆ A dan A ⊆ A, maka ∅ dan A disebut himpunan bagian tak sebenarnya (improper subset) dari himpunan A. Pernyataan A ⊆ B berbeda dengan A ⊂ B :
A ⊂ B : A adalah himpunan bagian dari B tetapi A ≠ B.
Yang demikian, A merupakan himpunan bagian sebenarnya (proper subset) dari B.

Contoh 11 :
Misalkan A = {1, 2, 3}.
{1} dan {2, 3} merupakan proper subset dari A.

Himpunan kuasa (power set) dari himpunan A merupakan suatu himpunan yang unsur-unsurnya merupakan semua himpunan bagian dari A, termasuk himpunan kosong dan himpunan A sendiri. Himpunan kuasa dinotasikan oleh P(A). Jumlah anggota (kardinal) dari suatu himpunan kuasa bergantung pada kardinal himpunan asal. Misalkan, kardinalitas himpunan A adalah m, maka ⏐P(A)⏐ = 2m.

Contoh 12 :
Jika A = { x, y }, maka P(A) = { ∅, { x }, { y }, { x, y }}
Contoh 13 :
Himpunan kuasa dari himpunan kosong adalah P(∅) = {∅}, sementara itu himpunan kuasa dari himpunan {∅} adalah P({∅}) = {∅, {∅}}.
Pernyataan A ⊆ B digunakan untuk menyatakan bahwa A adalah himpunan bagian (subset) dari B yang memungkinkan A = B.
Dua buah himpunan dikatakan sama jika memenuhi kondisi berikut :
A = B jika dan hanya jika setiap unsur A merupakan unsur B dan sebaliknya setiap unsur B merupakan unsur A.
Untuk menyatakan A = B, yang perlu dibuktikan adalah A adalah himpunan bagian dari B dan B merupakan himpunan bagian dari A. Jika tidak demikian, maka A ≠ B.
atau
A = B 􀃙 A ⊆ B dan B ⊆ A

Contoh 14 :
(i) Jika A = { 0, 1 } dan B = { x | x (x – 1) = 0 },
maka A = B
(ii) Jika A = { 3, 5, 8, 5 } dan B = {5, 3, 8 },
maka A = B
(iii) Jika A = { 3, 5, 8, 5 } dan B = {3, 8},
maka A ≠ B
Untuk tiga buah himpunan, A, B, dan C berlaku aksioma berikut:
(a) A = A, B = B, dan C = C
(b) Jika A = B, maka B = A
(c) Jika A = B dan B = C, maka A = C

Dua buah himpunan dikatakan ekivalen jika masing-masing mempunyai kardinalitas yang sama. Misalkan, himpunan A adalah ekivalen dengan himpunan B berarti kardinal dari
himpunan A dan himpunan B adalah sama, notasi yang digunakan adalah : A ~ B
Contoh 15 :
Misalkan A = { 2, 3, 5, 7 } dan B = { a, b, c, d },
maka A ~ B sebab ⏐A⏐ = ⏐B⏐ = 4
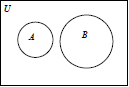
Dua himpunan A dan B dikatakan saling lepas (disjoint) jika keduanya tidak memiliki unsur yang sama. Notasi yang digunakan adalah A // B . Jika dinyatakan dalam bentuk diagram Venn adalah sebagai berikut :

Contoh 16 :
Jika A = { x | x ∈ N, x < 10 } dan B = { 11, 12, 13, 14, 15 },

maka A // B.

Operasi Himpunan

Ada beberapa operasi himpunan yang perlu diketahui, yaitu : irisan , gabungan, komplemen, selisih dan beda setangkup.

a. Irisan (intersection)

Irisan antara dua buah himpunan dinotasikan oleh tanda ‘∩ ‘.
Misalkan A dan B adalah himpunan yang tidak saling lepas, maka
A ∩ B = { x | x ∈ A dan x ∈ B }

Jika dinyatakan dalam bentuk diagram Venn adalah :

Contoh 17 :
1. Misalkan A = {2, 3, 5, 7, 11} dan B = {3, 6, 9, 12},
maka A ∩ B = {3}
2. Misalkan A adalah himpunan mahasiswi TI STT Telkom dan B merupakan
himpunan wanita lanjut usia (50 tahun ke atas)
maka A ∩ B = ∅.
Hal ini berarti A dan B adalah saling lepas atau A // B.

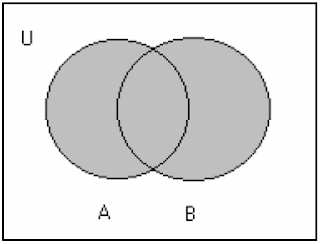
b. Gabungan (union)

Gabungan antara dua buah himpunan dinotasikan oleh tanda ‘∪‘.
Misalkan A dan B adalah himpunan, maka

A ∪ B = { x | x ∈ A atau x ∈ B }

Jika dinyatakan dalam bentuk diagram Venn adalah :
Contoh 18 :
(i) Jika A = { 2, 3, 5, 7} dan B = { 1, 2, 3, 4, 5 }, maka A ∪ B = { 1, 2, 3, 4, 5, 7}
(ii) A ∪ ∅ = A

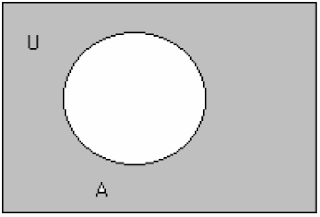
c. Komplemen (complement)

Komplemen dari suatu himpunan merupakan unsur -unsur yang ada pada himpunan
universal (semesta pembicaraan ) kecuali anggota himpunan tersebut. Misalkan A
merupakan himpunan yang berada pada semesta pembicaraan U, maka komplemen dari
himpunan A dinotasikan oleh : A = { x | x ∈ U dan x ∉ A }
Jika dinyatakan dalam b entuk diagram Venn adalah :

Contoh 19 :
Misalkan U = { 1, 2, 3, ..., 9 },
jika A = {1, 3, 7, 9}, maka A = {2, 4, 5, 6, 8}
jika A = { x ∈ U | x habis dibagi dua }, maka A= { 1, 3, 5, 7, 9 }

Contoh 20 :
A = himpunan mahasiswa STT Telkom
B = himpunan mahasiswa yang tinggal di Asrama
C = himpunan mahasiswa angkatan 2004
D = himpunan mahasiswa yang mengambil matematika diskrit
E = himpunan mahasiswa yang membawa motor untuk pergi ke kampus
a. Pernyataan
“Semua mahasiswa STT Telkom angkatan 2004 yang membawa motor untuk pergi ke kampus”
dapat dinyatakan dalam notasi operasi himpunan sebagai berikut :
(A ∩ C) ∩ E
b. Pernyataan
“Semua mahasiswa STT Telkom yang tinggal di asrama dan tidak mengambil matematika diskrit”
dapat dinyatakan dalam notasi operasi himpunan sebagai berikut :
A ∩ B ∩ D
c. Pernyataan
“semua mahasiswa angkatan 2004 yang tidak tinggal di asrama atau tidak membawa motor untuk pergi ke kampus”
dapat dinyatakan dalam notasi operasi himpunan sebagai berikut :
C ∩ (B ∪ E)

d. Selisih (difference)

Selisih antara dua buah himpunan dinotasikan oleh tanda ‘– ‘.
Misalkan A dan B adalah himpunan, maka selisih A dan B dinotasikan oleh
A – B = { x | x ∈ A dan x ∉ B } = A ∩ B

Contoh 21 :
Jika A = { 1, 2, 3, ..., 10 } dan B = { 2, 3, 5, 7}, maka A – B = { 1, 4, 6, 8, 9 }
dan B – A = ∅

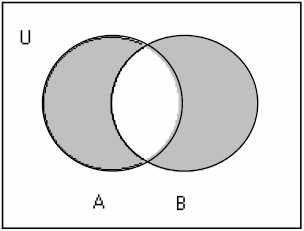
e. Beda Setangkup (Symmetric Difference)

Beda setangkup antara dua buah himpunan dinotasikan oleh tanda ‘ ⊕ ‘.
Misalkan A dan B adalah himpunan, maka beda setangkup antara A dan B dinotasikan
oleh :
A ⊕ B = (A ∪ B) – (A ∩ B)
= (A – B) ∪ (B – A)

Jika dinyatakan dalam bentuk diagram Venn adalah :Notasi:

Contoh 22 :
Jika A = { 2, 3, 5, 7} dan B = { 1, 2, 3, 4, 5 },
maka
A ⊕ B = { 1, 4, 7 }
Beda setangkup memenuhi sifat-sifat berikut:
(a) A ⊕ B = B ⊕ A (hukum komutatif)

(b) (A ⊕ B ) ⊕ C = A ⊕ (B ⊕ C ) (hukum asosiatif)

f. Perkalian Kartesian (cartesian product)

Perkalian kartesian antara dua buah himpunan dinotasikan oleh tanda ‘× ‘.
Misalkan A dan B adalah himpunan, maka perkalian kartesian antara A dan B
dinotasikan oleh :
A × B = {(a, b) ⏐ a ∈ A dan b ∈ B }
Contoh 23 :
(i) Misalkan C = {1, 2, 3}, dan D = { a, b }, maka
C × D = { (1, a), (1, b), (2, a), (2, b), (3, a), (3, b) }
(ii) Misalkan A = B = himpunan semua bilangan riil, maka
A × B = himpunan semua titik di bidang datar
Misalkan ada dua himpunan dengan kardinalitas berhingga, maka kardinalitas himpunan hasil dari suatu perkalian kartesian antara dua himpunan tersebut adalah perkalian antara kardinalitas masing-masing himpunan. Dengan demikian, jika A dan B merupakan himpunan berhingga, maka:
⏐A × B⏐ = ⏐A⏐ . ⏐B⏐.
Pasangan terurut (a, b) berbeda dengan (b, a), dengan kata lain (a, b) ≠ (b, a). Dengan
argumen ini berarti perkalian kartesian tidak komutatif, yaitu
A × B ≠ B × A
dimana A atau B bukan himpunan kosong.
Jika A = ∅ atau B = ∅, maka

A × B = B × A = ∅

Hukum-hukum yang berlaku untuk operasi himpunan adalah sebagai berikut :

1. Hukum identitas:
− A ∪ ∅ = A
− A ∩ U = A
2. Hukum null/dominasi:
− A ∩ ∅ = ∅
− A ∪ U = U
3. Hukum komplemen:
− A ∪ A = U
− A ∩ A = ∅
4. Hukum idempoten:
− A ∪ A = A
− A ∩ A = A
5. Hukum involusi:
)(A= A
6. Hukum penyerapan (absorpsi):
− A ∪ (A ∩ B) = A
− A ∩ (A ∪ B) = A
7. Hukum komutatif:
− A ∪ B = B ∪ A
− A ∩ B = B ∩ A
8. Hukum asosiatif:
− A ∪ (B ∪ C) = (A ∪ B) ∪ C
− A ∩ (B ∩ C) = (A ∩ B) ∩ C
9. Hukum distributif:
− A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
− A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
10. Hukum De Morgan:
− BA∩ = BA∪
− BA∪ = BA∩
11. Hukum komplemen
− ∅ = U

Share on Google Plus

About hariabri

Cari materi belajar ? clocarius edu tempatnya.