Penjelasan Algoritma A* beserta contoh kasus algortima A*

Penjelasan Algoritma A* beserta contoh kasus algortima A* - Algoritma menjadi salah satu hal yang sangat penting untuk membangun suatu sistem yang baik. Pada mata kuliah kecerdasan buatan dan juga strategi algoritma biasanya penggunaan algortima A* atau A star cukup sering digunakan untuk menyelesaikan suatu permasalahan tertentu. Karena itulah artikel ini saya buat agar teman-teman semua dapat membaca dan mempelajari tentang algoritma A* atau A star.

Penjelasan Algoritma A*

A* atau yang biasa juga disebut dengan algoritma A star adalah salah satu algoritma yang dapat digunakan untuk menentukan total minimum biaya lintasan dan juga saat kondisi yang tepat dapat memberikan solusi yang optimal. Cara kerja dari algoritma ini hampir sama dengan algoritma best first search, akan tetapi di modifikasi dengan fungsi heuristik.

Algoritma A star memerlukan dua model antrian yaitu antrian open dan juga antrian closed. Modifikasi dari fungsi heuristik dari algoritma A* dapat melakukan prediksi pada setiap node-node yang dibuat. Langkah ini dilakukan agar memudahkan algoritma tersebut untuk menentukan langkah-langkah selanjutnya yang di harapkan. Cara tersebut dapat disimbolkan dengan fungsi f’(n) sebagai pendekatan terhadap fungsi f(n) dimana fungsi f(n) adalah fungsi evaluasi yang sebenarnya terhadap node (n).

Pada banyak kasus akan jauh lebih baik jika suatu fungsi di definisikan menjadi suatu kombinasi ataupun jumlah dari dua atau lebih komponen yaitu g(n) dan h(n). Fungsi g(n) adalah ukuran dari biaya yang telah dikeluarkan dari suatu keadaan awal hingga ke node (n). Hasil dari g(n) tersebut bukan merupakan hasil dari estimasi melainkan jumlah dari biaya penerapan setiap aturan yang dilakukan sepanjang lintasan terbaik yang telah ditentukan dengan fungsi heuristik yang menuju suatu simpul.

Untuk fungsi dari h(n) adalah ukuran dari biaya tambahan yang mesti dikeluarkan dari node (n) hingga mencapai tujuan. Sebagai catatan, fungsi dari g(n) tidak boleh negatif karena jika negatif maka lintasan yang membalik siklus pada graf akan terlihat lebih baik dengan semakin panjangnya jumlah dari lintasan.

Rumusan Formula A*

Untuk fungsi matematisnya dapat dituliskan seperti berikut:
f(n) = g(n) + h’(n)

Keterangan :
f(n) : fungsi dari evaluasi
g(n) : biaya yang telah dikeluarkan dari keadaan awal hingga node (n)
h’(n) : estimasi dari biaya yang dikeluarkan dari keadaan n atau node (n) hingga sampai ke tujuan.
Jika h = h’, maka proses dari pencarian tersebut telah mencapai tujuannya (goal).
Jika g = h’ = 0 maka f’ random, yang berarti sistem tersebut tidak bisa untuk dikendalikan. 
Jika g = k, k adalah konstanta dan biasanya bernilai 1, h’ = 0, yang berarti sistem tersebut menggunakan teknik best first search.

Contoh kasus Algoritma A*

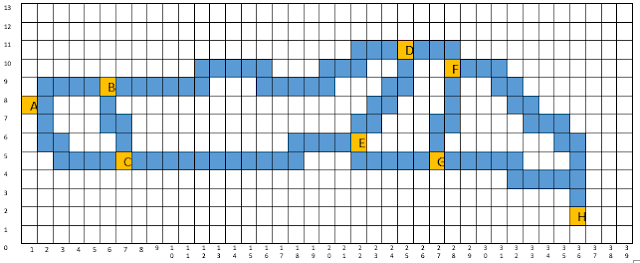
Diberikan suatu kasus seperti gambar, jika seorang pengendara akan pergi berkeliling dari pontianak menuju ke melawi hingga kembali ke pontianak, manakah rute yang paling optimal untuk dilalui oleh si pengendara ? Dalam hal ini rute optimal adalah jarak tercepat untuk dilalui dari pontianak-melawi-pontianak.

Langkah pertama tentukan nilai dari h'(n) dengan menggunakan rumus dua titik :

Perhitungan:
A ke B = (2,14), (14,19) = 13
A ke C = (2,14), (38,15) = 36,01
A ke D = (2,14), (32,4) = 31,62
A ke E = (2,14) , (13,5) = 14,21
B ke A = (14,19), (2,14) = 13
B ke C =(14,19), (38,15) = 24,33
B ke D = (14,19), (32,4) = 23,43
B ke E = (14,19), (13,5) = 14,04
C ke A = (38,15), (1,14) = 36,01
C ke B = (38,15), (14,19) = 24,33
C ke D = (38,15), (32,4) = 12,43
C ke E = (38,15), (13,5) = 26,93
D ke A = (32,4), (1,14) = 31,62
D ke B = (32,4), (14,19) = 23,43
D ke C = (32,4), (38,15) = 12,53
D ke E = (32,4), (13,5) = 19,03
E ke A = (13,5), (1,14) = 14,21
E ke B = (13,5), (14,19) = 14,04
E ke C = (13,5), (38,15) = 26,93
E ke D = (13,5), (32,4) = 19,03
 

Setelah itu mencari nilai f(n). g(n) didapat dari mengukur jarak antara 1 point ke point lainnya lalu mencari nilai f(n) dengan rumus f(n)=h’(n)+g(n):

A ke B = 13  + 18 = 31
A ke C =  36,01 + 37 = 73,01
A ke D =  31,62 + 40 = 71,62
A ke E =  14,21 + 20 = 34,21
B ke A = 13 + 18 = 31
B ke C = 24,33 + 29 = 53,33
B ke D = 23,43 + 34 = 57,43
B ke E = 14,04 + 16 = 30,04
C ke A = 36,01 + 37 = 73,01
C ke B = 24,33 + 29 = 53,33
C ke D = 12,43 + 17 = 29,43
C ke E = 26,93 + 35 = 61,93
D ke A = 31,62 + 40 = 71,62
D ke B = 23,43 + 34 = 57,43
D ke C = 2,53 + 17 = 29,43
D ke E = 19,03 + 20 = 39,03
E ke A = 14,21 + 20 = 34,21
E ke B = 14,04 + 16 = 30,04
E ke C = 26,93 + 35 = 61,93
E ke D = 19,03 + 20 = 39,03

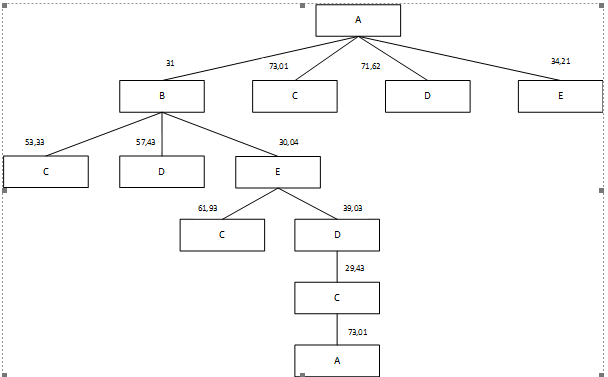
Setelah f(n) telah didapatkan, gambarkan rute perjalanan. Setiap pemilihan rute dilakukan dengan memilih nilai terkecil

Dari gambar diatas, kita temukan rute terbaik dari metode ini adalah A-B-E-D-C-A.

Contoh soal Algoritma A* 2 :

1 Indeks berjarak 150 Meter
A = Rumah Sakit Soedarso
B = Perempatan Jl. Mayor Alianyang
C = Bundaran Jl. Arteri Supadio
D = Pertigaan Jl. Parit Bugis dan Jl. Adisucipto
E = Pertigaan Jl. Parit Bugis dan Jl. Arteri Supadio
F = Pertigaan Jl. Wonodadi dan Jl. Adisucipto
G = Pertigaan Jl. Wonodadi dan Jl. Arteri Supadio
H = Bandara Supadio

Nilai Heuristik
A ke B (0,8) (6,9) = 6,08
A ke C (0,8),(7,5) = 7,62
B ke D (6,9),(25,11) = 19,10
B ke C (6,9),(7,5) = 4,12
C ke B (7,5),(6,9) = 4,12
C ke E (7,5),(22,6) = 15,03
D ke F (25,11),(28,10) = 3,16
D ke E (25,11),(22,6) = 5,83
E ke D (22,6),(25,11) = 5,83
E ke G (22,6),(27,5) = 5,10
F ke G (28,10),(27,5) = 5,10
F ke H (28,10),(36,2) = 11,31
G ke F (27,5),(28,10) = 5,10
G ke H (27,5),(36,2) = 9,49

Nilai f(n)
A ke B = 6+6,08 = 12,08
A ke C = 9+7,62 =  16,62
B ke D = 23+19,10 = 42,10
B ke C = 5+4,12 = 9,12
C ke B = 5+4,12 = 9,12
C ke E = 16+15,03 = 31,03
D ke F = 4+3,16 = 7,16
D ke E = 8+5,83 = 13,83
E ke D = 8+5,83 = 13,83
E ke G = 6+5,10 = 11,10
F ke G = 6+5,10 = 11,10
F ke H = 16+ 11,31 = 27,31
G ke F = 6+5,10 = 11,10
G ke H = 12+9,49 = 21,49

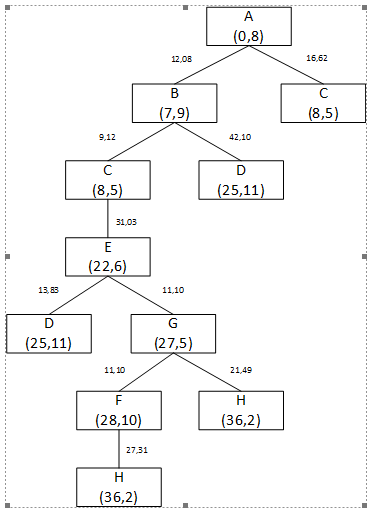
Jalur yang dilalui adalah A-B-C-E-G-F-H

Total f(n) = 12,08+9,12+31,03+11,10+11,10+27,31 = 101,74

Share on Google Plus

About hariabri

Cari materi belajar ? clocarius edu tempatnya.